Abstract

Image quality assessment (IQA) models aim to establish a quantitative relationship between visual images and their perceptual quality by human observers. IQA modeling plays a special bridging role between vision science and engineering practice, both as a test-bed for vision theories and computational biovision models, and as a powerful tool that could potentially make profound impact on a broad range of image processing, computer vision, and computer graphics applications, for design, optimization, and evaluation purposes. IQA research has enjoyed an accelerated growth in the past two decades. Here we present an overview of IQA methods from a Bayesian perspective, with the goals of unifying a wide spectrum of IQA approaches under a common framework and providing useful references to fundamental concepts accessible to vision scientists and image processing practitioners. We discuss the implications of the successes and limitations of modern IQA methods for biological vision and the prospect for vision science to inform the design of future artificial vision systems.

The Bayesian Interpretation of Objective IQA

Given a set of training data D comprising n input images (and optionally some side-information) X=(x1,...,xn) and their corresponding target quality scores y=(y1,...,yn), the goal of objective IQA is to find a posterior quality distribution p(y|x,D) that best approximates p(y|x) in the human visual system (HVS). By assuming the training data are independent and identically distributed, the predictive distribution can be parametrized as p(y|x,D)=∫p(y|x,θ)p(θ|D)dθ, where θ, p(y|x,θ) and p(θ|D) represent the parameters of the HVS model, the quality rating generation process and the posterior distribution over parameters, respectively. Given the enormous space of θ, the computation of the integral is prohibitively expensive. As a result, a common practice is to approximate the predictive distribution p(y|x,D) by a point estimate p(y|x,θ∗), where θ∗=arg⁡maxθp(θ|D)=arg⁡maxθp(y|X,θ)p(θ). The specific form of the likelihood function p(y|X,θ) is not known in practice. To fully specify the problem, it is usually assumed that the likelihood function follows a Gaussian distribution.

Direct estimation of θ from a set of training data is problematic, because of the fundamental conflict between the enormous size of the image space and the limited scale of affordable subjective testing. As a result, the fundamental problem in the objective IQA is to develop a meaningful prior parameter distribution p(θ), which encodes the configuration of the HVS.

Over the past decades, various IQA models have been developed where the key difference lies in the assumptions about the prior distribution p(θ). In general, three types of knowledge may be used for the design of image quality measures, as shown in the figure below.

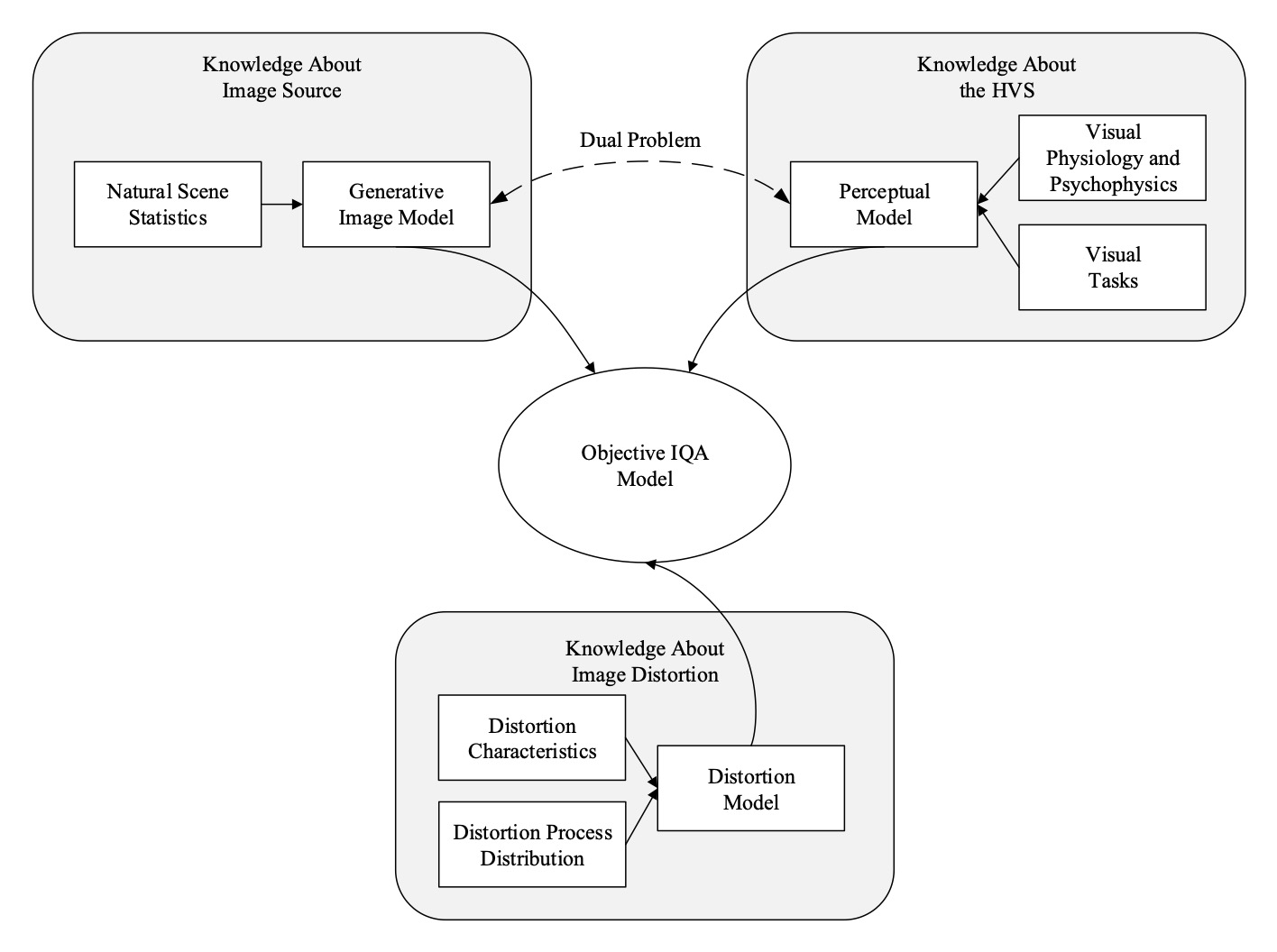
Based on the types of knowledge on which an IQA model relies, we derive a new taxonomy of objective IQA models.

Select Model
Project Paper Code
Model Full Name
  • A short description.
Knowledge Pool
Natural Scene Statistics Distortion Characteristics Distortion Process Distribution Visual Physiology and Psychophysics Visual Tasks
Select Dataset
  • Dataset description.
Project
Paper
Code
Distortion Types
Authentic AWGN GBLUR JPEG JP2K FF Chroma Noise Pink Noise Masked Noise High Freq Noise Impluse Noise Quant. Noise Denoising JPEG Trans. Error JP2K Trans. Error Non-Eccent. Noise Block Dist. Mean Shift Contrast Dist. Sat. Dist. Multi. Noise Comfort Noise Dithering Chroma Aber. Super Res. LAR Coding Multiply Dist. Poisson Noise Lens Blur Motion Blur Color Diffusion Color Shift Color Quantization AWGN YCbCr Impulse Noise Multiplicative Noise Brighten Darken Jitter Pixelate Color Block High Sharpen
Downloads

Preprint

Official Version
Citation
@article{duanmu2021biqa,
        author = {Duanmu, Zhengfang and Liu, Wentao and Wang, Zhongling and Wang, Zhou},
        title = {Quantifying Visual Image Quality: A Bayesian View},
        journal = {Annual Review of Vision Science},
        volume = {7},
        number = {1},
        pages = {437-464},
        year = {2021}
        }