Given a set of training data \(\mathcal{D}\) comprising \(n\) input images (and optionally some side-information) \({\bf X} = ({\bf x}_1, . . . , {\bf x}_n)\) and their corresponding target quality scores \({\bf y} = (y_1, . . . , y_n)\), the goal of objective IQA is to find a posterior quality distribution \(p(y|{\bf x}, \mathcal{D})\) that best approximates \(p(y|{\bf x})\) in the human visual system (HVS). By assuming the training data are independent and identically distributed, the predictive distribution can be parametrized as \[p(y|{\bf x}, \mathcal{D}) = \int p(y|{\bf x}, \theta) p(\theta|\mathcal{D}) d\theta,\] where \(\theta\), \(p(y|{\bf x}, \theta)\) and \(p(\theta|\mathcal{D})\) represent the parameters of the HVS model, the quality rating generation process and the posterior distribution over parameters, respectively. Given the enormous space of \(\theta\), the computation of the integral is prohibitively expensive. As a result, a common practice is to approximate the predictive distribution \(p(y|{\bf x}, \mathcal{D})\) by a point estimate \(p(y|{\bf x}, \theta^*)\), where \[\theta^* = \arg\max_{\theta} p(\theta|\mathcal{D}) = \arg\max_{\theta} p({\bf y}|{\bf X}, \theta) p(\theta).\] The specific form of the likelihood function \(p({\bf y}|{\bf X}, \theta)\) is not known in practice. To fully specify the problem, it is usually assumed that the likelihood function follows a Gaussian distribution.
Direct estimation of \(\theta\) from a set of training data is problematic, because of the fundamental conflict between the enormous size of the image space and the limited scale of affordable subjective testing. As a result, the fundamental problem in the objective IQA is to develop a meaningful prior parameter distribution \(p(\theta)\), which encodes the configuration of the HVS.
Over the past decades, various IQA models have been developed where the key difference lies in the assumptions about the prior distribution \(p(\theta)\). In general, three types of knowledge may be used for the design of image quality measures, as shown in the figure below.
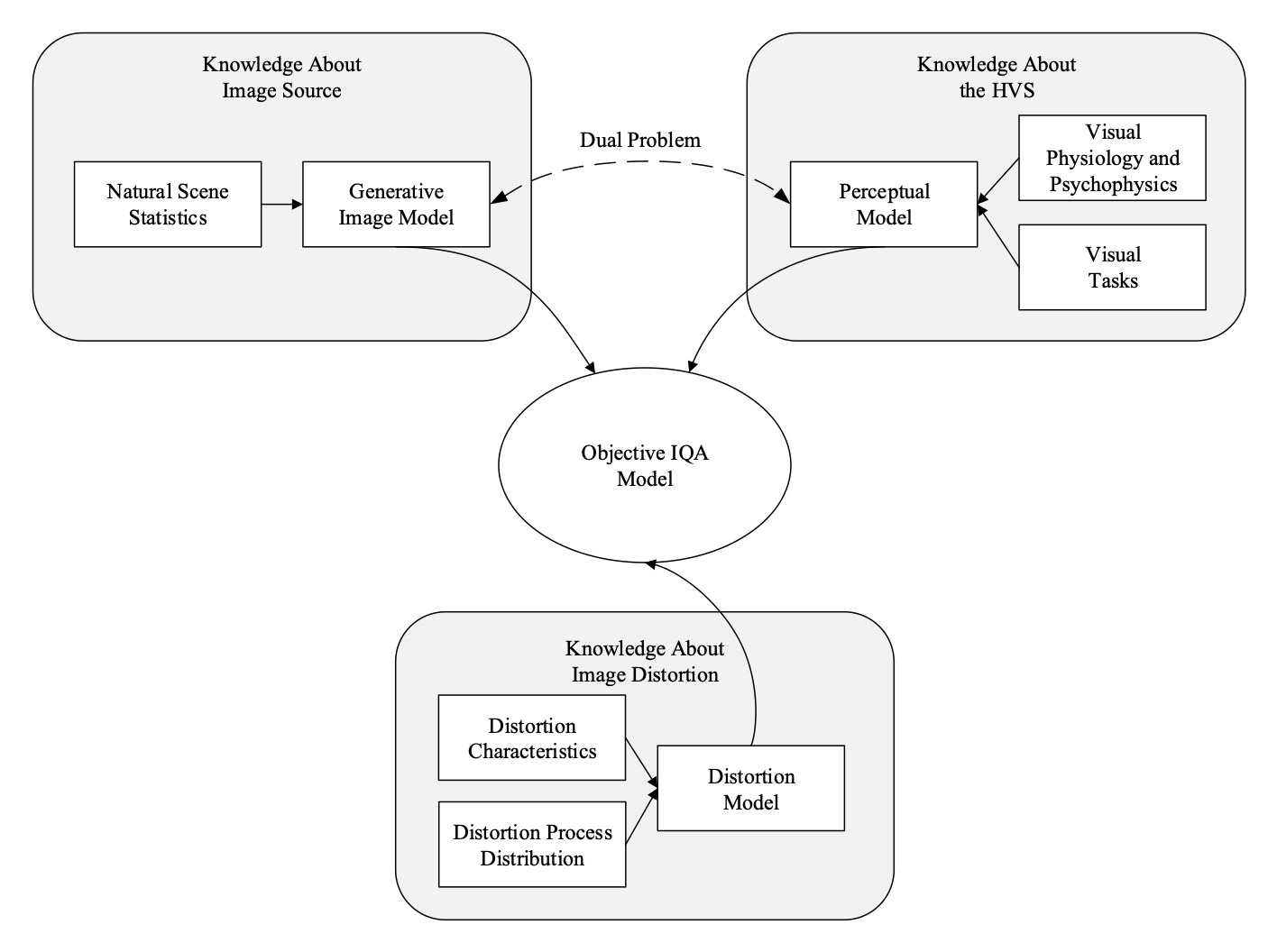
Based on the types of knowledge on which an IQA model relies, we derive a new taxonomy of objective IQA models.